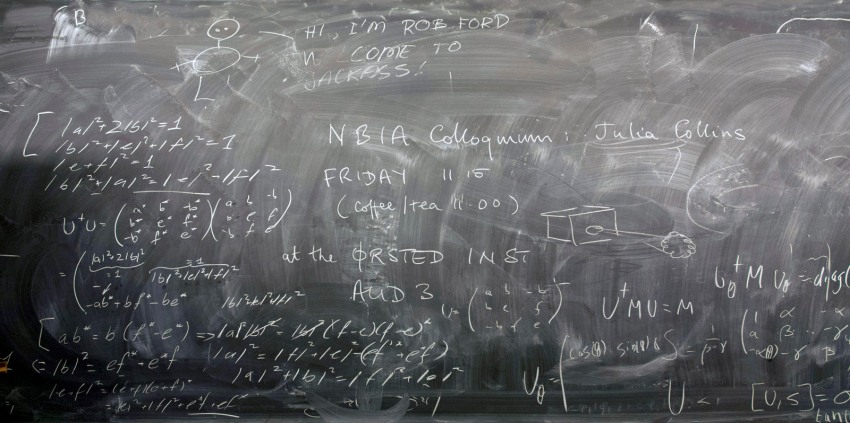Accidental pies

This is the blackboard from the University of Edinburgh School of Mathematics common room from September 2015. I particularly noticed it because of the inadvertent appearance of P(ies) in the centre! I’m also enjoying the idea of pulsational energy.

Don Zagier on modular forms

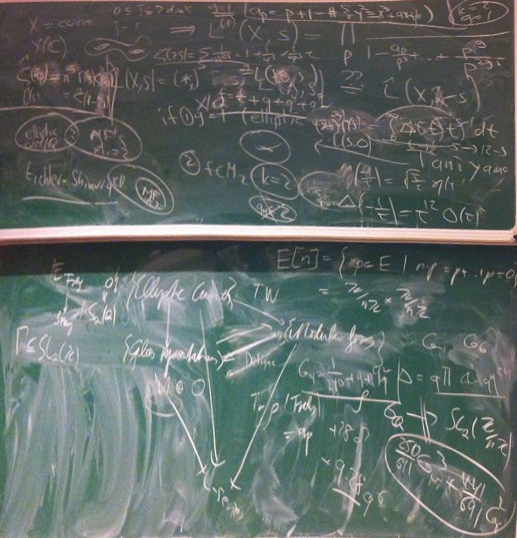Théophile Cantelobre, a student at the Lycée Louis-le-Grand, sent me this photo from a summer school he’s been attending in Bremen. He writes:

“Yesterday night, we had an improvised lecture by Don Zagier introducing us to modular forms. Ben Heuer, a PhD student in number theory in London, continued on to finish an explanation started earlier about the connections between elliptic curves, Galois representation and modular forms and notably the implications towards Fermat’s Last Theorem.

A friend of mine (Richard) took a picture of the board… it’s a special one: a lecture given by Don Zagier with John Conway in the audience!”

It certainly looks like an exciting and dynamic lecture judging by the board!

Shape optimization

I found this board at the International Centre for Mathematical Sciences (ICMS) during a conference about shape optimisation and shape geometry. Talking to some of the delegates there I found out that the field is all about finding the best shapes to suit a purpose, and these purposes might come from physics, engineering, architecture, or simply pure mathematics. For example, the Reuleaux triangle is a shape of constant width (it has the same diameter wherever you measure it) but has an area 12% less than a circle of the same diameter. This makes it more efficient for making coins (our 50p piece is a similar shape but with 7 sides), manhole covers and even buildings.

I asked conference delegate Jimmy Lamboley what his favourite shape was, and he laughed and said “Anything but a sphere!”. He explained: ” The sphere is so often the answer to minimisation problems that I love to find the problems where it isn’t the case.”

The Reuleaux triangle is a great example of a shape more efficient than a circle. What’s amazing is that the corresponding question for 3D shapes (which shape of constant width has minimum volume?) is a problem still waiting for a solution.

Fractal decorations

I found this blackboard in the maths common room of Lafayette College, a beautiful old campus university near the small town of Easton (just north of Philadelphia in the US). While the board contains some nice mathematics, I was particularly taken by the psychedelic fractal border on top of the board. I believe this was created by Professor Cliff Reiter, who has done a lot of research into visualisation and fractals, and who has an interesting textbook on the subject.

Combinatorics of non-crossing partitions

The board is a result of of Bin Shu from East China Normal University visiting Iain Gordon at the University of Edinburgh. In Iain’s words: “We were discussing the combinatorics of non-crossing partitions, and its generalisations to a bunch of different finite groups. The two diagrams are Cayley graphs of symmetric groups where one calculates this combinatorics. Most of that text is in black, but we were lazybones, so there is also a bit of green writing from my PhD student, about braid group actions on tensor categories and their asymptotic limits. Amazingly, the two topics are linked, through moduli spaces in algebraic geometry!”

Board of pi

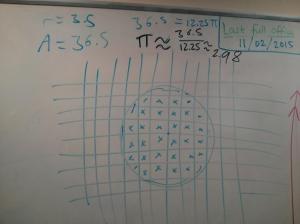
This board by David Cushing at Newcastle University attempts to calculate pi very crudely by counting how many squares a circle covers and using the formula

Area = pi x r²

to get a value of 2.98. Can you do better?

This exercise was part of a series of activities carried out to celebrate “Ultimate pi day” on 3/14/15 (in US date format). There were also many other attempts by people to  estimate the value of pi using nonstandard methods. Did you take part in the festivities and, if so, how?

Backward differential equations

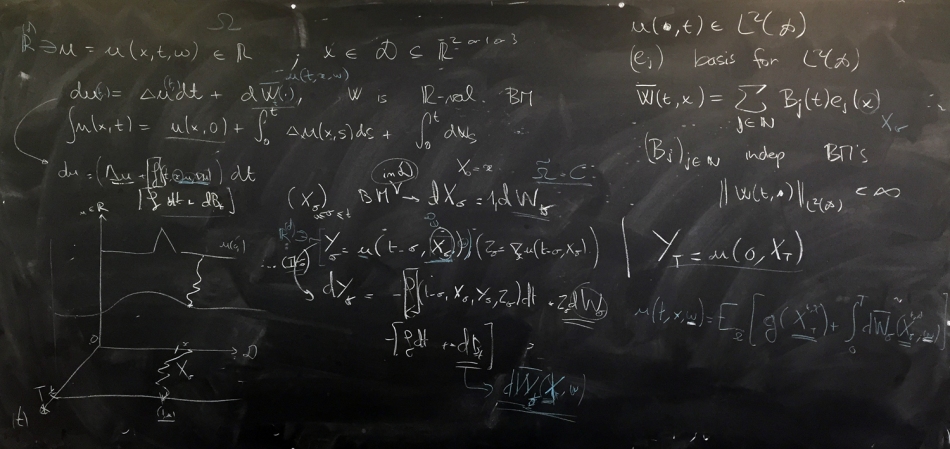This board was created in the common room of the School of Mathematics at the University of Edinburgh by David Siska and Arnaud Lionnet. Arnaud is visiting David in Edinburgh, and they are working on backward stochastic differential equations and stochastic partial differential equations, which are on the interface between probability and analysis.

Self-intersection numbers for a fence

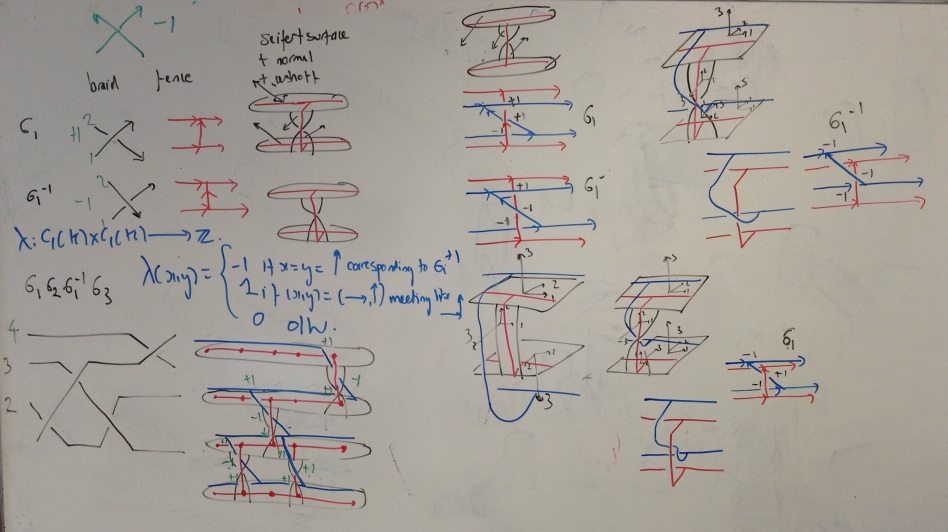This is the board of Chris Palmer, a postgraduate at the University of Edinburgh. He has recently been working on finding a simple chain level Seifert pairing for the Seifert surface of a link. This is related to his supervisor Andrew Ranicki’s recent talk in which he used surgery theory to find a chain level pairing. The figures show how to compute the self intersection numbers for a fence (a one-dimensional simplicial complex that is a deformation retraction of the Seifert surface).

Backdrop for Sir Michael Atiyah

Today the University of Edinburgh was privileged to welcome award-winning photographer James Glossop to the School of Mathematics. His task was to photograph Sir Michael Atiyah for an article in The Times (to appear next week) and he asked for a blackboard to be decorated with mathematical equations to form the backdrop to this photo. It was a joint effort between Andrew Ranicki, Julia Collins, Patrick Orson, and (of course) Sir Michael, and contains all their favourite formulae, numbers and ideas in mathematics. What would you have drawn on the board?

James kindly took this photo of the board after he was finished getting his shots of Sir Michael. I like the heavenly light shining in from above!

Niels Bohr Institute

This is the blackboard in the common room at the Niels Bohr Institute in Copenhagen, taken by Andrew Jackson. It is advertising a colloquium given by Julia Collins about Peter Guthrie Tait, with a helpful diagram of a vortex cannon to show people what to expect in the talk.  Unrelatedly, there is a lot of matrix algebra on the left and what seems to be a half-rubbed-off torus on the right. Proof that even in a physics institute, much of the work is really mathematics! We have no idea what the cartoon at the top signifies.